Write Better: Discussions
Discussions - what are they?
After sharing the results from your experiment, and analysed them graphically with graphs, the trends and patterns are examined in more detail in the discussion section, along with an analysis of the method used.
Analysing the Data
Before you make any calculations and look for trends or patterns in the data, the anomalies in the results need to be identified and explained. They can often be explained by any observations you have made during the course of conducting the experiment. Once you have identified these anomalies, you need to discount/disregard them from your calculations such that they do not affect your findings.
After sharing the results from your experiment, and analysed them graphically with graphs, the trends and patterns are examined in more detail in the discussion section, along with an analysis of the method used.
- Analyse the data for trends, patterns, and anomalies
- Analyse the data for accuracy - design/measurement errors and how significant they are
- Analyse the method - your design - what worked well, and what changes could be made to improve the accuracy and reliability next time.
Analysing the Data
Before you make any calculations and look for trends or patterns in the data, the anomalies in the results need to be identified and explained. They can often be explained by any observations you have made during the course of conducting the experiment. Once you have identified these anomalies, you need to discount/disregard them from your calculations such that they do not affect your findings.
|
Table 2: Average Mario Kart Time Scores
Anomalies Example 1: "When testing each student's average time score on Mario Kart, it was found that one of Student A's time trials (34.21min) was much greater than the rest of his time trials (2.48 - 3.14mins) (Table 2). This is likely because at some point during testing, his mother called him on the phone and he needed time to explain why he wasn't at Student's D's house, studying, like he said he would be."
In this case, it would not be fair to count the anomaly in Student A's time trial data, so we would calculate his average time without it:
Student A Average Time = (2.48 + 3.14)s ÷ 2
∴ Student A Average Time = 2.81s |
Table 4: Sulfur content in Fertiliser
Anomalies Example 2: "The 1.02g sample of fertiliser trial, produced a yield of 12.9% Sulfur, which is much less than the rest of the data which ranges between 14.0-16.5% Sulfur (Table 4). This loss of Sulfur product was likely due to some of the sample being lost when pouring off the excess water from the beaker in step 7 of the method, which could have carried away some of the solids down into the sink."
So for the sulfur % in the fertiliser experiment, we would not count the anomaly of 12.9% in our calculations, like the average sulfur percentage:
Average % sulfur = (16.5 + 16.2 + 14.0 + 15.0)g ÷ 4
∴ Average % sulfur = 15.4g |
In most cases, it is important to show at least one or two sample calculations (like the ones above). This will demonstrate your ability to do these calculations, to the teacher, or in some other cases - explain what mumbo-jumbo math magic you just pulled to find these numbers! (that will probably be more applicable to senior students).
Once the anomalies have been omitted, examine the measurements and figures from your results table(s) and graphs to identify any trends. It is really important to refer to which table the results are from, and using specific results to show evidence of the trends that you have found.
Trend Example 1: "From table 1, the results showed that students who had the least energy intake for breakfast (300kJ), also had the lowest numbers of kills when playing the game of Call of Duty (3 kills), whereas the students who had eaten plenty for breakfast (8000kJ), performed better (>9000 kills)."
Trend Example 2: "As the drop height increased from 0.500m to 1.500m, the average bounce height also increased from 0.187m up to 0.493m (table 1)."
Trend Example 2: "As the drop height increased from 0.500m to 1.500m, the average bounce height also increased from 0.187m up to 0.493m (table 1)."
Then, examine the graph(s) you have made and draw a line of best fit (trend line), determine if this line shows a linear/exponential/logarithmic relationship between your variables.
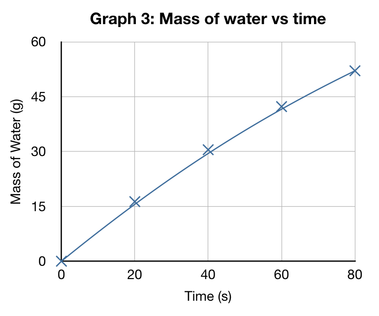
Trend line analysis (junior): Graph 3 shows that as the time increases, so does the mass of water collected by a similar amount for every 20 seconds. The slope of the trend line starts quite steeply, but decreases towards the end of the graph at 80 seconds.
Trend line analysis (senior): The line of best fit in Graph 3 begins at a steep gradient and later tapers off at a shallower gradient towards the end of the graph. This suggests that the Mass of water collected over time shows a logarithmic relationship, which could be modelled by the formula; y = aLog (bx + 1). (Ideally, you would have this calculated and fitted onto the graph opposite, but I haven't had the time).
Trend line analysis (senior): The line of best fit in Graph 3 begins at a steep gradient and later tapers off at a shallower gradient towards the end of the graph. This suggests that the Mass of water collected over time shows a logarithmic relationship, which could be modelled by the formula; y = aLog (bx + 1). (Ideally, you would have this calculated and fitted onto the graph opposite, but I haven't had the time).
Sometimes the data does not show a linear or exponential relationship, but may oscillate - like a pattern:
Pattern Example: "Table 1 reveals that flood depth of the creek cycles from 0.0m in the winter up to 1.3m during Summer and then down again to 0.0m the following winter. The plot on Graph 1 of flood depth over 3 years suggests that this pattern repeats every year for the creek."
Once you have identified the trends or patterns in the data, now explain what these results mean, and reason why this may have been the case.
Meaning Example 1: "The differences in performance in the results of students who had limited or plenty of caloric intake for breakfast, suggests that for peak performance for Call of Duty, students need to have a healthy breakfast meal with sufficient calories."
Analysing Errors
Errors are NOT mistakes! Often when we collect and analyse our results from experiments we find that our results are off by a small or large amount. Error analysis is a discussion of where the source of these differences could come from; and this will come from a collection of the following:
Together, these will contribute to how far off our findings are from what is true or accepted (e.g. it is generally accepted that the value of π is 3.14159..., the accepted boiling point of water is 100°C, and the accepted value for the acceleration due to Earth's gravity, g = 9.81m/s²). Note: your experiment may not have an 'accepted value' to compare with, but you should still consider this process of error analysis anyway to evaluate the primary sources of error that could have affected your results.
For example, in an experiment designed to measure the acceleration due to gravity, using a stopwatch and an inclined plane, it was calculated from the results obtained that the value for Earth's gravity was not the same as the accepted value (9.81m/s²).
Errors are NOT mistakes! Often when we collect and analyse our results from experiments we find that our results are off by a small or large amount. Error analysis is a discussion of where the source of these differences could come from; and this will come from a collection of the following:
- Equipment accuracy - some equipment is more precise than others; a 250mL measuring cylinder has more detail on the exact volumes used, than a 250mL beaker which may have only about 3-5 increments marked on it
- Experimental design - perhaps there are some losses because your design did not capture/collect/measure it all.
Together, these will contribute to how far off our findings are from what is true or accepted (e.g. it is generally accepted that the value of π is 3.14159..., the accepted boiling point of water is 100°C, and the accepted value for the acceleration due to Earth's gravity, g = 9.81m/s²). Note: your experiment may not have an 'accepted value' to compare with, but you should still consider this process of error analysis anyway to evaluate the primary sources of error that could have affected your results.
For example, in an experiment designed to measure the acceleration due to gravity, using a stopwatch and an inclined plane, it was calculated from the results obtained that the value for Earth's gravity was not the same as the accepted value (9.81m/s²).
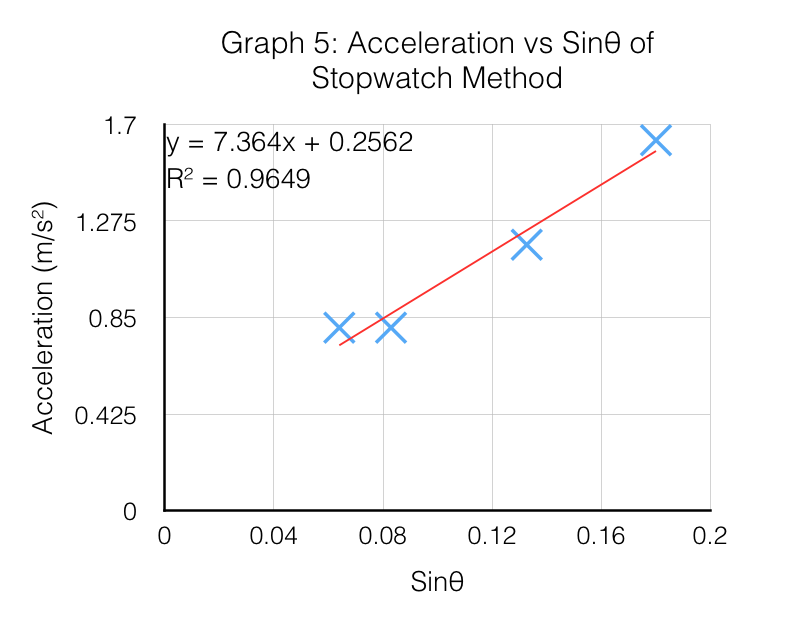
Mathematically, (I'm going to skip the physics in-between because that's not the point for this illustration), g can be found by examining the slope of the graph, in Graph 5. This shows that experimentally, g is 7.364 m/s² instead of the accepted value of 9.81m/s². How far off our result is, is known as the experimental error.
Experimental Error (%) = |Accepted value - Experimental value| ÷ Accepted value x 100%
For example:
Experimental Error (%) = |9.81m/s² - 7.364m/s²| / 9.81m/s² x 100%
Experimental Error (%) = 24.9%
For example:
Experimental Error (%) = |9.81m/s² - 7.364m/s²| / 9.81m/s² x 100%
Experimental Error (%) = 24.9%
Now that the experimental error has been calculated, we find that our result for g is 24.9% less than the accepted value. To discuss why this has occurred, we examine the equipment involved, and the design. The more detailed your error analysis, the better. I'll provide only a brief example (since this scenario is similar to a school assessment item).
Error Analysis (equipment) Example 1: "The experimental error of this investigation shows a difference of 24.9% less than the accepted value of the acceleration due to gravity of 9.81m/s². This implies that the measured acceleration of the car rolling down the incline was slower than it should be. This cannot be fully explained by the error of the stopwatch used; which involves a short time delay to react to a stimulus (the car begins to roll down) to start it, and another time delay to react when the car has reached the end of the plank. Human reaction times with stopwatches when testing was found to be approximately 0.16s, which accumulates each time the operator presses the button on the stop watch. In this case, twice (start + stop), which results in a time delay of approximately 0.32s. Although 0.32s is a significant time relative to the average times taken to roll down the plank (1.61 - 2.29s), this delay would likely have offset the measurements. For example, the timer is started 0.16s after the cart begins to roll, and 0.16s after the car has reached the end of the plank. The primary source of the experimental error is likely to have been caused by... (more measurement limitations, design limitations, etc)."
Error Analysis (design) Example 2: "After examining the measured amount energy released per biscuit (average of 1.37kJ per biscuit), and comparing this result with the accepted value of the package (53.7kJ per biscuit), it was found that the experimental results from the investigation deviated from the accepted value by 97.4%. This discrepancy is most likely due to the design of the experiment; it was assumed that the heat generated from the combustion (burning) of the biscuit (click here to see the video) would be captured and measured by the test tube + thermometer that was stationed above the flames from the biscuit. This design did not account for the heat generated and lost to the surroundings because although hot air rises, it is not the only means of which heat is transmitted. Heat energy is known to transfer via radiation as well, which operates in all directions - not just above. Therefore, much of the heat generated by the combustion of the biscuit was not captured and measured by the test-tube and thermometer apparatus."
Error Analysis (equipment) Example 1: "The experimental error of this investigation shows a difference of 24.9% less than the accepted value of the acceleration due to gravity of 9.81m/s². This implies that the measured acceleration of the car rolling down the incline was slower than it should be. This cannot be fully explained by the error of the stopwatch used; which involves a short time delay to react to a stimulus (the car begins to roll down) to start it, and another time delay to react when the car has reached the end of the plank. Human reaction times with stopwatches when testing was found to be approximately 0.16s, which accumulates each time the operator presses the button on the stop watch. In this case, twice (start + stop), which results in a time delay of approximately 0.32s. Although 0.32s is a significant time relative to the average times taken to roll down the plank (1.61 - 2.29s), this delay would likely have offset the measurements. For example, the timer is started 0.16s after the cart begins to roll, and 0.16s after the car has reached the end of the plank. The primary source of the experimental error is likely to have been caused by... (more measurement limitations, design limitations, etc)."
Error Analysis (design) Example 2: "After examining the measured amount energy released per biscuit (average of 1.37kJ per biscuit), and comparing this result with the accepted value of the package (53.7kJ per biscuit), it was found that the experimental results from the investigation deviated from the accepted value by 97.4%. This discrepancy is most likely due to the design of the experiment; it was assumed that the heat generated from the combustion (burning) of the biscuit (click here to see the video) would be captured and measured by the test tube + thermometer that was stationed above the flames from the biscuit. This design did not account for the heat generated and lost to the surroundings because although hot air rises, it is not the only means of which heat is transmitted. Heat energy is known to transfer via radiation as well, which operates in all directions - not just above. Therefore, much of the heat generated by the combustion of the biscuit was not captured and measured by the test-tube and thermometer apparatus."
Evaluating the Method
Experiments are often repeated by other scientists at a later date to verify your results (checking that you haven't made everything up!), and also they are often expanded upon to take the research further. Your role, as having completed this experiment - is to evaluate your design for what worked well and what could be improved to increase the accuracy (0.1m vs 0.100345m) , eliminate or reduce chances of errors (heat loss, etc), and improve the reliability (fool proof; works every time).
Method Evaluation (accuracy) Example: The thermometer provided accurate measurements for large changes in temperature (20-50°C), however a digital temperature probe could be used in the future to show greater precision of temperature changes with more significant figures. For example, the thermometer, at best, can measure to 1/2 a degree; 24.5°C, whereas a digital temperature probe can measure temperatures with more detail (24.492°C) and record these changes over time. The maximum temperature could therefore be more easily identified in cases where the test tube apparatus may start to cool down after the biscuit has finished burning.
Method Evaluation (errors) Example:
The use of the test tube filled with 10mL of water and a thermometer to capture the heat generated from the combustion of the biscuit was not very effective, as most of the heat was lost to the surroundings. In future experiments, this issue could be addressed by insulating the region of space around the biscuit and test-tube apparatus such as a cardboard box lined with woollen cloth. Wool is commonly used to retain heat in clothing during the winter and is fire-resistant, and so should not burn in the case that the flames from the biscuit would make contact with the insulation. The cardboard box could have an opening on the bottom and the top to allow air, and the necessary oxygen, to flow up towards the flame, and out the top for the combustion to continue to work.
Method Evaluation (reliability) Example:
The large variation of results between the heat energy collected from each biscuit suggests that the current design is not very reliable. This may have occurred due to the difficulty in centring all the flames of the biscuit underneath the test-tube apparatus. To improve the consistency of results, the biscuits could be crushed into a powder, poured into a small pile, and lit with a match such that the flames created could be more easily centred underneath the test tube apparatus.
Experiments are often repeated by other scientists at a later date to verify your results (checking that you haven't made everything up!), and also they are often expanded upon to take the research further. Your role, as having completed this experiment - is to evaluate your design for what worked well and what could be improved to increase the accuracy (0.1m vs 0.100345m) , eliminate or reduce chances of errors (heat loss, etc), and improve the reliability (fool proof; works every time).
Method Evaluation (accuracy) Example: The thermometer provided accurate measurements for large changes in temperature (20-50°C), however a digital temperature probe could be used in the future to show greater precision of temperature changes with more significant figures. For example, the thermometer, at best, can measure to 1/2 a degree; 24.5°C, whereas a digital temperature probe can measure temperatures with more detail (24.492°C) and record these changes over time. The maximum temperature could therefore be more easily identified in cases where the test tube apparatus may start to cool down after the biscuit has finished burning.
Method Evaluation (errors) Example:
The use of the test tube filled with 10mL of water and a thermometer to capture the heat generated from the combustion of the biscuit was not very effective, as most of the heat was lost to the surroundings. In future experiments, this issue could be addressed by insulating the region of space around the biscuit and test-tube apparatus such as a cardboard box lined with woollen cloth. Wool is commonly used to retain heat in clothing during the winter and is fire-resistant, and so should not burn in the case that the flames from the biscuit would make contact with the insulation. The cardboard box could have an opening on the bottom and the top to allow air, and the necessary oxygen, to flow up towards the flame, and out the top for the combustion to continue to work.
Method Evaluation (reliability) Example:
The large variation of results between the heat energy collected from each biscuit suggests that the current design is not very reliable. This may have occurred due to the difficulty in centring all the flames of the biscuit underneath the test-tube apparatus. To improve the consistency of results, the biscuits could be crushed into a powder, poured into a small pile, and lit with a match such that the flames created could be more easily centred underneath the test tube apparatus.
Wrapping things up
That's pretty much it. You may be asked to embellish your discussion with
Common Mistakes
When grading student papers, it's common to see that they mistakenly use first person voice - especially since you are discussing your own findings, however please remember to always maintain consistent formal scientific language - past tense, passive voice, and 3rd person. Or more simply put; write it as formal as possible.
That's pretty much it. You may be asked to embellish your discussion with
- Links to other literature
- Implications/relevance to the real world
- Link results back to the hypothesis
Common Mistakes
When grading student papers, it's common to see that they mistakenly use first person voice - especially since you are discussing your own findings, however please remember to always maintain consistent formal scientific language - past tense, passive voice, and 3rd person. Or more simply put; write it as formal as possible.